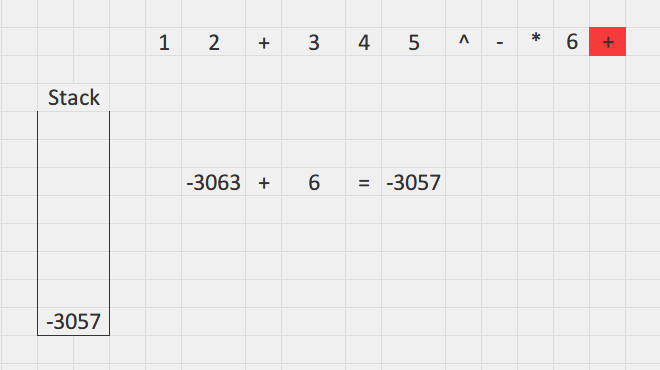[教程][算法] Infix 转 Postfix
29 May 2015简介
Infix 表达式就是平常我们常用的,用来表达一个算术/方程式表达式的方式
比如说:
A + B * C - D
A + B * ( C + D * E)
( ( A + B ) * ( C - D ^ E) + F)
等等……
但是Infix(中缀表示法)对电脑来说太难处理了,所以就有了Postfix(或称Reversed Polish notation, RPN, 后缀表示法)
A + B * C - D
A + B * ( C + D * E)
( ( A + B ) * ( C - D ^ E) + F)
上述例子的Postfix 就是:
A B C * + D -
A B C D E * + * +
A B + C D E ^ - * F +
Postfix如何计算值
例子1:
在解释如何从Infix转Postfix之前,向来看看Postfix表达式如何求值:
A B C * + D -
看成:
1 2 3 * + 4 -
就是 1 + 2 * 3 - 4
现在有一个stack,专门储存operand
还有一个pointer,每次都向前移动一个字符(图片中被高亮起来的)
用图解释吧:
1 被入stack
2 被入栈
push 3
现在遇到一个operator
因为乘法需要两个operand,所以pop两个operator
然后进行运算,运算结果被push
加法,同理
push 4
pop 两个
进行运算 (顺序很重要!)
然后push
接下来pointer抵达尾端,pop出
运算结果便是3
例子2:
A B + C D E ^ - * F +
看成这样吧:
1 2 + 3 4 5 ^ - * 6 +
( ( 1 + 2 ) * ( 3 - 4 ^ 5 ) + 6 )
Infix 转 Postfix
首先就是priority 列表:
( )
* /
- + -
基本流程是这样的:
- 若当前pointer指着的是一个operand,直接print出
- 若当前pointer指着的是一个operator:
- 若stack为空,push 入该operator
- 若stack最上方为
(,push 入该operator - 若当前operator为
),pop stack 并且print出,一直到遇到另一个(为止。(然后pop(,并且(和)皆不print出) - 若当前operator的优先权高过stack最上方的operator,push 入该operator
- 若当前operator的优先权低过stack最上方的operator,pop stack的最上方,继续进行优先权比较,直到遇到一个比当前operator优先权低的operator为止。
- 若当前operator与stack最上方的operator同一优先权,pop stack再print出,然后push 入当前operator
- pointer抵达尾端后,pop出所有stack内的operator(
(除外)
例子1:
A + B * C + D - E / F
1 + 2 * 3 + 4 - 5 / 5
例子2:
( ( A + B ) * ( C - D ^ E ) + F )
( ( 1 + 2 ) * ( 3 - 4 ^ 5 ) + 6 )
static string infixToPostfix(string exp)
{
Dictionary<char, int> priority = new Dictionary<char, int>()
{
{'(',4},{')',4},{'^',3},{'*',2},{'/',2},{'+',1},{'-',1}
};
Stack<char> opt = new Stack<char>();
string postfix = "";
foreach (char c in exp)
{
if (priority.ContainsKey(c))
{
if (opt.Count == 0)
{
opt.Push(c);
}
else
{
if (c == ')')
{
while (opt.Count > 0 && opt.Peek() != '(')
{
postfix += opt.Pop();
}
opt.Pop();
}
else if (opt.Peek() == '(')
{
opt.Push(c);
}
else if (priority[c] > priority[opt.Peek()])
{
opt.Push(c);
}
else if (priority[c] < priority[opt.Peek()])
{
while (opt.Count > 0 && priority[c] <= priority[opt.Peek()] && opt.Peek()!='(')
{
postfix += opt.Pop();
}
opt.Push(c);
}
else if (priority[c] == priority[opt.Peek()])
{
postfix += opt.Pop();
opt.Push(c);
}
}
}
else
{
postfix += c.ToString().Trim();
}
}
while (opt.Count > 0)
{
postfix += opt.Pop();
}
return postfix;
}